Template Meta Programming으로 matrix 라이브러리 만들기 (2)

이전 포스팅에서는 TMP를 적용하면 좋은 점에 대해 알아보았다. 이제 실제 구현한 코드를 보며 행렬의 덧셈까지 구현해보자.

1. MatrixExpr 클래스

Expression template의 아이디어는 모든 행렬과 식을 각각 고유한 타입으로 나타내는 것이다. Expression을 나타낼 클래스를 이렇게 구현했다.

template <typename E>
struct MatrixExpr{
    inline auto elem(Index r, Index c) const{
        return static_cast<const E&>(*this).elem(r, c);
    }

    inline auto& elem(Index r, Index c) {
        return static_cast<const E&>(*this).elem(r, c);
    }

    static constexpr Index row = E::row;
    static constexpr Index col = E::col;
};

(링크)

앞으로 구현할 모든 클래스는 이 MatrixExpr 클래스를 상속받을 것이다. 두 elem() 메소드는 행/열 index를 인자로 받아 그에 해당하는 lvalue, rvalue를 리턴한다. 이 MatrixExpr 클래스가 일종의 인터페이스 역할을 한다고 할 수 있다. 그런데 두 가지 이상한 점이 눈에 띄는데, 보통의 base class의 그것과는 달리 virtual method가 없는 것, 그리고 이전 포스트에는 없던 템플릿 인자를 하나 받고 있는 것이다.

이는 흔히 볼 수 있는 virtual function을 이용한 override와 달리 컴파일 시간에 이루어지는 static polymorphism을 쓰기 위한 CRTP (Curiously Recurring Template Pattern)을 이용하기 위함이다. 자세한 설명은 생략하고, MatrixExpr을 상속받는 클래스들은 다음과 같이 자기 자신을 템플릿 인자로 받는 클래스를 상속받는 꼴을 갖는다.

struct A : public MatrixExpr<A>{
	...
};

MatrixExpr에서는 static_cast를 이용해 자식 클래스의 메소드를 바로 호출할 수 있다. static_cast는 컴파일 타임에 동작하므로, 결과적으로 자식 클래스의 메소드를 컴파일 타임에 결정할 수 있다.

elem() 함수는 row, col Index를 인자로 갖는다. 호출되면 해당 위치의 element의 값을 계산해서 return한다. 앞선 포스팅에서 계산한 값이 필요할 때만 계산을 한다고 했는데, 그 때 이 함수가 호출이 될 것이다. 

2. Matrix 클래스

가장 중요한 클래스인 Matrix 클래스를 살펴보자. 전체 코드중에서 operator+() 구현에 필요한 부분만 간추렸다.

먼저 Matrix 클래스는 자료형, 행/열의 수를 템플릿 인자로 받는다. 이 때 Row, Col은 0보다 커야 하고, 자료형은 수를 나타내는 타입이어야 한다. 이를 requires를 이용해 컴파일 타임에 확인한다.

template<typename T, Index Row, Index Col>
    requires std::is_arithmetic_v<T> && (Row > 0) && (Col > 0)
struct Matrix : public MatrixExpr<Matrix<T, Row, Col>>{
	// ...
};

이제 템플릿 인자로 받은 것들을 MatrixExpr에서 요구하는 constexpr 변수로 지정해야 한다. Row, Col 말고도 T를 나타내는 변수를 지정해야 하는데 C++에서는 타입을 저장하는 자료형이 없다. 따라서 코드로 element type을 저장하도록 강제를 할 수는 없었고 대신 MatrixExpr 주석에서 `Type` 으로 alias를 만들기로 명시하였다.

using Type = T;
static constexpr Index row = Row;
static constexpr Index col = Col;

Matrix는 임의의 expression으로부터 생성될 수 있어야 한다. 이전 포스트에서 실제 계산하는 값이 필요할 때 한꺼번에 계산을 한다고 했는데 (lazy evaluation), 이는 MatrixExpr을 갖는 Matrix 생성자를 만들어 구현할 수 있다. MatrixExpr 인터페이스의 elem()을 호출해서 각 element의 값을 계산하고 이를 대입한다.

template<typename E>
Matrix(const MatrixExpr<E> &expr) requires is_equal_type_size_v<E, Matrix>{
    for(Index r=0;r<Row;r++){
        for(Index c=0;c<Col;c++){
            elem(r, c) = expr.elem(r, c);
        }
    }
}

 

Matrix 클래스의 elem() 함수는 계산할 필요가 없이 해당 위치의 lvalue/rvalue 를 return하면 된다.

inline T elem(Index r, Index c) const{
    return m_data[Col*r+c];
}

inline T& elem(Index r, Index c) {
    return m_data[Col*r+c];
}

위 코드들을 모으면 다음과 같다.

template<typename T, Index Row, Index Col>
    requires std::is_arithmetic_v<T> && (Row > 0) && (Col > 0)
struct Matrix : public MatrixExpr<Matrix<T, Row, Col>>{
    using Type = T;
    static constexpr Index row = Row;
    static constexpr Index col = Col;
    
    template <typename ...TList> requires std::conjunction_v<std::is_same<T, TList>...>
    Matrix(TList ... tlist) : m_data{std::forward<T>(tlist)...} {}

    template<typename E>
    Matrix(const MatrixExpr<E> &expr) requires is_equal_type_size_v<E, Matrix>{
        for(Index r=0;r<Row;r++){
            for(Index c=0;c<Col;c++){
                elem(r, c) = expr.elem(r, c);
            }
        }
    }

    inline T elem(Index r, Index c) const{
        return m_data[Col*r+c];
    }

    inline T& elem(Index r, Index c) {
        return m_data[Col*r+c];
    }

private:
    std::array<T, Row*Col> m_data;
};

3. MatrixSum 클래스

이제 임의의 MatrixExpr 간의 덧셈을 나타내는 MatrixSum를 구현해보자. MatrixSum 클래스는 임의의 expression type 두 개 (E1, E2)를 템플릿 파라미터로 갖는다. Matrix와 마찬가지로 CRTP를 위해 자기 자신을 템플릿 인자로 갖는 MatrixExpr을 상속받는다. 이때 E1, E2의 행렬의 크기가 같아야 하는데, 이는 is_equal_size_mav_v 를 구현해 컴파일 시간에 체크하도록 했다 (링크). 

template<typename E1, typename E2>
    requires is_equal_size_mat_v<E1, E2>
struct MatrixSum : public MatrixExpr<MatrixSum<E1, E2>> {
	// ...
};

Matrix와 마찬가지로 row, col, Type을 정의한다. E1, E2의 크기가 같으므로 E1의 row, col을 사용한다.

using Type = typename E1::Type;
static constexpr Index row = E1::row;
static constexpr Index col = E1::col;

MatrixSum 클래스는 E1, E2 타입의 멤버 레퍼런스 x, y를 갖는다. 레퍼런스이기 때문에 인자로 들어온 전체 행렬을 복사하지 않는다.

MatrixSum(const E1 &x, const E2 &y) : x{x}, y{y} {}

const E1 &x;
const E2 &y;

MatrixSum의 elem() 함수는 두 멤버의 각 index에 해당하는 값을 더한 후 return하면 된다. 이때 x의 elem(), y의 elem()이 재귀적으로 호출되면서 적절한 값을 evaluation할 것이다.

// Static polymorphism implementation of MatrixExpr
inline auto elem(Index r, Index c) const {
    return x.elem(r, c) + y.elem(r, c);
}

전체 코드는 다음과 같다.

template<typename E1, typename E2>
    requires is_equal_size_mat_v<E1, E2>
struct MatrixSum : public MatrixExpr<MatrixSum<E1, E2>> {
    using Type = typename E1::Type;
    MatrixSum(const E1 &x, const E2 &y) : x{x}, y{y} {}

    // Static polymorphism implementation of MatrixExpr
    inline auto elem(Index r, Index c) const {
        return x.elem(r, c) + y.elem(r, c);
    }

    static constexpr Index row = E1::row;
    static constexpr Index col = E1::col;

    const E1 &x;
    const E2 &y;
};

3.1 operator+() 함수

이제 남은건 MatrixSum을 만들어 return하는 함수 operator+()를 만드는 것이다. MatrixSum과 동일한 템플릿 인자를 받고, 임의의 MatrixExpr 인자 두 개(MatrixExpr<E1>, MatrixExpr<E2>)를 받아서, 그 자식 클래스 (E1, E2)로 형변환 후 MatrixSum을 생성하게 한다. 역시 static_cast를 사용했기 때문에 실행 시간에서의 손해는 없다.

template<typename E1, typename E2>
    requires is_equal_size_mat_v<E1, E2>
MatrixSum<E1, E2> operator+(const MatrixExpr<E1> &x, const MatrixExpr<E2> &y) {
    return MatrixSum<E1, E2>(static_cast<const E1 &>(x), static_cast<const E2 &>(y));
}

4. 결과

Expression tree 생성과 evaluation이 되는 모습

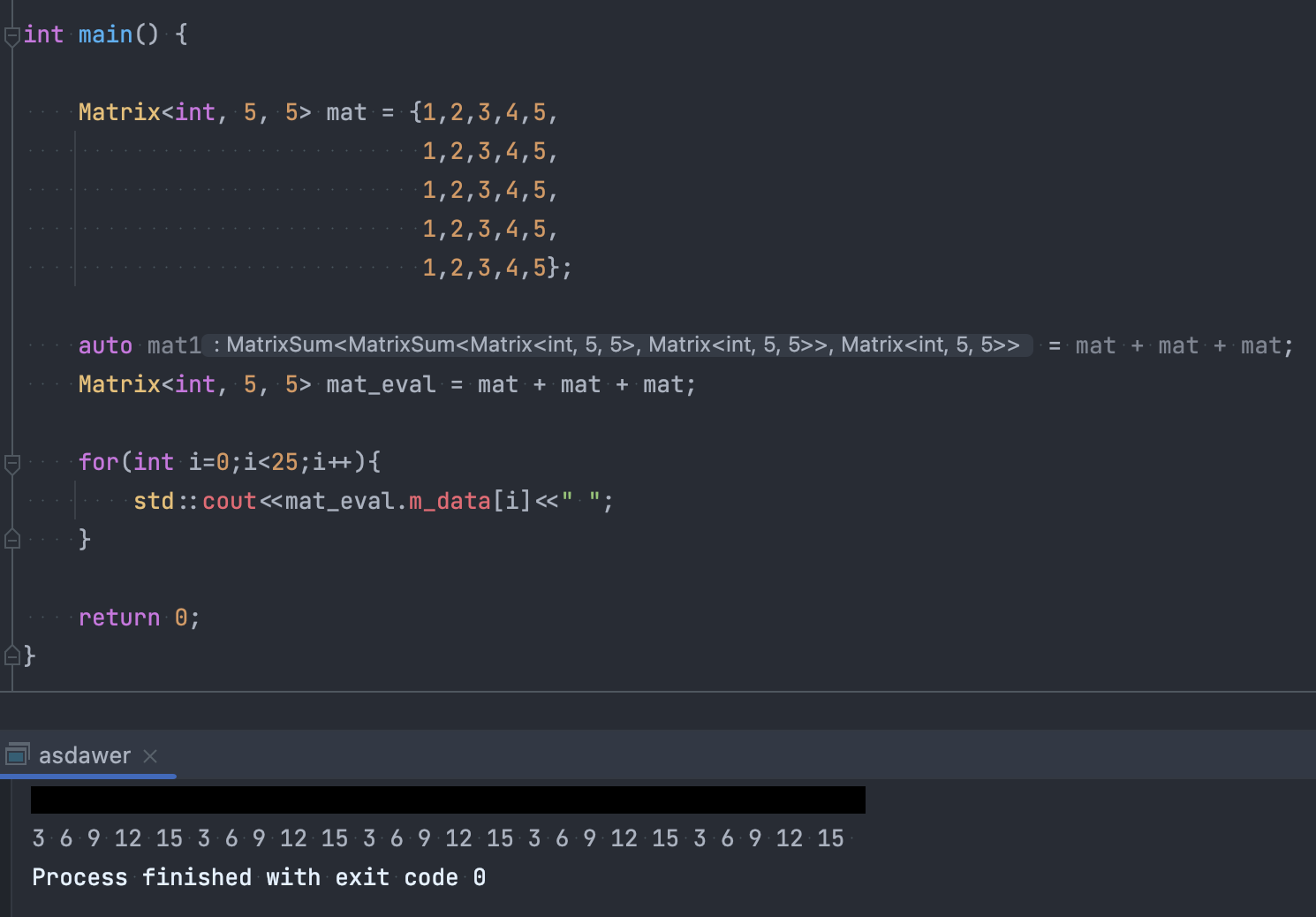
Reference

https://github.com/pjessesco/peanut/blob/72c261c79fdf79ba865a467f54bb3468d8e7025c/Peanut/impl/matrix.h

https://github.com/pjessesco/peanut/blob/72c261c79fdf79ba865a467f54bb3468d8e7025c/Peanut/impl/binary_expr/matrix_sum.h

https://github.com/pjessesco/peanut/blob/72c261c79fdf79ba865a467f54bb3468d8e7025c/Peanut/impl/matrix_type_traits.h