--- 2021/6/25 수정 : 코드 관련 부분 삭제
이번 Assignment는 기존에 사용하지 않았던 `Emitter`, `BSDF`를 이용한 렌더링 알고리즘을 구현한다. Distribution Ray Tracing과 Whitted-style Ray Tracing이다.
시작하기 전에 Assignment 2에서 구현했던 `accel.cpp`와 `accel.h`를 대체하는 코드를 받았다. 내꺼랑 다르게 진짜 빠르다..
1. Area lights
저번 Assignment에서 다룬 Point Light는 사실 물리적으로 불가능한 형태의 광원이다. 모든 물체는 면적이 있기 때문이다. 여기서는 조금 더 현실적인 Area Light를 구현하기 위한 준비를 한다.
XML 파일에서 Area Light는 다음과 같이 나타난다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
<scene>
<!-- Load a OBJ file named "bunny.obj" -->
<mesh type="obj">
<string name="filename" value="bunny.obj"/>
<!-- Turn the mesh into an area light source -->
<emitter type="area">
<!-- Assign a uniform radiance of 1 W/m2sr -->
<color name="radiance" value="1, 1, 1"/>
</emitter>
</mesh>
<!-- ..... -->
</scene>
|
cs |
이를 파싱하기 위해 우선 아래와 같은 `AreaLight` 클래스를 `src/area.cpp`에 만들었다. 위의 XML파일에 있는 radiance를 생성자에서 저장한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
#include <nori/common.h>
#include <nori/emitter.h>
NORI_NAMESPACE_BEGIN
class AreaLight :Emitter{
public:
AreaLight(const PropertyList &plist){
m_radiance = plist.getColor("radiance");
}
private:
Color3f m_radiance;
};
NORI_REGISTER_CLASS(AreaLight, "area");
NORI_NAMESPACE_END
|
cs |
다음에 구현할 Distribution Ray Tracing을 구현하기 위해서 `AreaLight` 위의 점을 uniform하게 sampling할 수 있어야 한다고 한다. `Mesh` 클래스에 다음 기능을 하는 함수를 구현한다.
- Mesh 위의 한 점을 sampling하기.
- 그 점에서의 노멀 벡터를 점에서의 노멀 벡터를 통해 계산하기. Mesh에 노멀 벡터가 없으면 면의 노멀 벡터를 계산하기.
- sampling한 점이 나올 확률을 계산하기.
`nori/mesh.h`에 `samplePosition()` 함수가 선언되어 있었다.
|
1
|
void Mesh::samplePosition(const Point2f &sample, Point3f &p, Normal3f &n) const;
|
cs |
sample의 확률을 반환할 수 없었기 때문에, 아래와 같이 선언을 수정했다.
|
1
|
float Mesh::samplePosition(const Point2f &sample, Point3f &p, Normal3f &n) const;
|
cs |
`Mesh::samplePosition()`을 구현하는 데에 `nori/dpdf.h`에 구현되어 있는 `DiscretePDF`를 이용했다. 이 클래스는 내가 float값을 차례대로 넣으면 , 그 비율에 따라 index를 sampling해준다.
Mesh 위의 점을 sampling하는 방법은 우선 Mesh를 이루는 삼각형을 먼저 선택하고, 뽑은 삼각형 안에서 uniform하게 점을 뽑는다. 삼각형을 선택할때 삼각형의 넓이가 모두 다르기 때문에 `DiscretePDF`를 이용해 face의 넓이에 비례하는 확률로 sampling했다. Mesh의 멤버 변수 `m_dpdf`는 `Mesh::activate()`에서 구성된다.
삼각형 하나를 sampling하기 위해 `Mesh::activate()`에서 만든 `m_dpdf`를 이용한다. 하지만 우리가 이 함수에서 사용해야 하는 랜덤 변수는 3개인데(삼각형을 sampling 할 때 하나, 삼각형 위의 점을 sampling할 때 두 개), `Mesh::samplePosition()`는 Point2f를 파라미터로 받는다. 즉 우리가 받는 랜덤 변수는 2가지 뿐이다. 다행히도 `DiscretePDF`는 샘플링에 쓰인 랜덤 변수를 변환해 다시 우리가 샘플링하는데 쓸 수 있게 해주는 기능을 제공한다.
|
1
|
const size_t sample_index = m_dpdf.sampleReuse(sample1);
|
cs |
이제 Sampling한 삼각형 face 위의 점을 uniform하게 sampling 해야 한다. Assignment에 제시된

는 [0,1] X [0,1] 을 (1,0,0), (0,1,0), (0,0,1) 을 꼭짓점으로 갖는 삼각형 안의 점(P)으로 uniform 하게 변환한다. (1,0,0), (0,1,0), (0,0,1)을 sampling된 삼각형의 각 꼭짓점(P0, P1, P2)으로 변환하는 행렬(A)을 찾아서 P를 A로 변환한 AP를 구하면 sampling한 삼각형 안에서 sampling된 점의 좌표를 구할 수 있다.
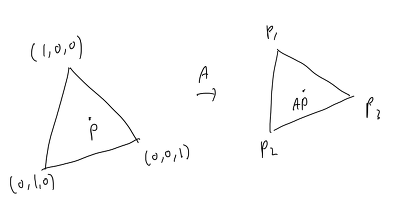
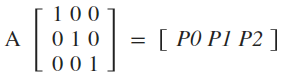
여기서 A는 [P0, P1, P2] 와 같음을 쉽게 알 수 있다.
구하고자 하는 AP, 즉 uniform하게 sampling된 삼각형 안의 점의 좌표는 다음과 같이 구할 수 있다.
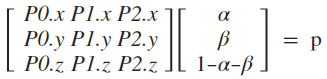
Mesh에 꼭짓점의 노멀 벡터가 있으면, sampling한 점의 노멀 벡터는 각 꼭짓점의 노멀 벡터를 interpolation 하면 된다. 생각해보면, P의 좌표는 곧 (1,0,0), (0,1,0), (0,0,1)을 일정 비율로 interpolation한 결과이다. P에서의 노멀 벡터는 (1,0,0), (0,1,0), (0,0,1)의 노멀 벡터를 같은 비율로 interpolation한 결과와 같을 것이다.
P0, P1, P2에서의 노멀 벡터를 각각 N0, N1, N2라고 하자. sampling한 삼각형 위의 점 AP에서의 노멀 벡터는 곧 N0, N1, N2를 P의 좌표값인 P.x, P.y, P.z의 비율로 interpolation한 것과 같음을 알 수 있다. 이때 P.x, P.y, P.z는 `b_x`, `b_y`, `b_z`와 같다. P에서의 노멀 벡터를 A로 변형시키지 않는 이유는, 노멀 벡터를 변형한 벡터가 변형된 면의 노멀 벡터가 아니기 때문이다.
만약 Mesh에 꼭짓점의 노멀 벡터 정보가 없으면, 두 벡터의 외적을 통해 면의 노멀 벡터를 계산할 수 있다.
sampling한 점이 나올 확률은
1 / (전체 Mesh의 면적)
과 같다. `Mesh::samplePosition()`에서 확률을 반환하게 했다.
전체 `Mesh::samplePosition()`는 다음과 같다.
2. Distribution Ray Tracing
알고리즘을 구현하기 위한 준비가 끝났고, 이제 새로운 렌더링 알고리즘을 구현할 차례이다. 새로운 Integrator인 whitted.cpp를 생성했다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
#include <nori/integrator.h>
NORI_NAMESPACE_BEGIN
class WhittedIntegrator : public Integrator {
public:
WhittedIntegrator(const PropertyList &props) {
}
Color3f Li(const Scene *scene, Sampler *sampler, const Ray3f &ray) const {
return Color3f(0.0f);
}
std::string toString() const {
return "WhittedIntegrator[]";
}
};
NORI_REGISTER_CLASS(WhittedIntegrator, "whitted");
NORI_NAMESPACE_END
|
cs |
이 Integrator는 기본적으로 다음을 계산하면 된다고 한다.
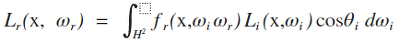
X는 렌더링이 될 점, wi는 X에서 광원으로의 방향, wr은 X에서 카메라로의 방향이다. Θi는 X에서의 법선 벡터와 wi 사이의 각도이다. fr(X, wi, wr)은 물질이 X에서 wi로 오는 빛을 wr로 얼마나 반사하는지 나타내는 함수이고, Li(X, wi)는 X에서 wi 방향으로 도달하는 radiance를 나타낸다. H2는 X를 시점으로 하는 모든 방향, 즉 X를 중심으로 하는 반구를 뜻한다. 주의할 점은, 위의 식 뿐만 아니라 앞으로 나오는 모든 벡터는 보통 점으로 들어가는 방향이 아니라 점에서부터 나가는 방향을 의미한다.

이 적분식에 의하면, 어떤 점을 렌더링하기 위해서는 그 점으로 향하는 모든 방향에 대해 점으로 오는 radiance를 찾고, 특정 방향에서 온 빛이 카메라로 반사되는 비율을 곱해서 모두 더하면 된다.
하지만 위 식은 조금만 생각해보면 비효율적이라는 것을 알 수 있다. 점에서 어떤 방향에 광원이 있을 줄 알고 모든 방향에 대해 적분을 하는가? 광원의 수가 적다면 전체 방향 중 소수만이 의미있는 방향이 될 것이다. 또한 선택한 방향이 어떤 광원에 영향을 받는지 하나하나 검사하는 것도 비효율적이다.
(20-01-07 추가 : 비교를 위해 whitted_mats를 추가했음)

효율적으로 구현하는 방법은, 점의 모든 방향에 대해 적분하는 대신 광원 위의 임의의 점에서 X가 보이는지 확인하는 것이다.
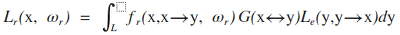
L은 광원의 표면이고, y는 광원의 표면 위의 한 점이다. 즉 광원 위의 모든 점 y에 대해서, y에서 x로 향하는 radiance를 fr과 곱하고, dw를 dy로 바꾸는 과정에서 생긴 Geometric term G를 곱한다. 여기서 G는 다음과 같다.

G는 뒤에서 다시 살펴보자.
효율적인 방법과 비효율적인 방법의 가장 큰 차이는, 점 x로 들어오는 radiance를 필요로 하는지, 점 y에서 나오는 radiance를 필요로 하는지이다. L 밑의 첨자가 i와 e로 다른 것을 확인할 수 있다. Li는 incident radiance, Le는 emitted radiance를 뜻한다.
fr은 BSDF::eval()을 이용해 쉽게 구할 수 있다. 우리가 구현해야 하는건 G와 Le인데, 먼저 Le를 구현하기 위해 Emitter의 인터페이스를 구성해야 한다.
인터페이스 구성을 위해 PBRT의 내용이나 코드, 그리고 Mitsuba Renderer의 인터페이스를 많이 참고했다. PBRT에선 위에서 언급한 내용을 나누어 인터페이스를 구성했다. 점 X로 들어오는 radiance는 Sample_Li()로, 광원 위의 점 y에서 나오는 radiance는 Sample_Le()로 구할 수 있다. 우리가 비효율적인 방법으로 구현한다면 Sample_Li()를 구현해야 했겠지만, 여기선 Sample_Le()만 구현하면 된다.
다음은 PBRT의 Sample_Le()의 선언이다.
|
1
2
3
|
virtual Spectrum Sample_Le(const Point2f &u1, const Point2f &u2, Float time,
Ray *ray, Normal3f *nLight, Float *pdfPos,
Float *pdfDir) const = 0;
|
cs |
우리가 필요없는 파라미터를 빼고, 포인터 파라미터를 참조 파라미터로 옮기는 등 정리를 하면, 내 Sample_Le() 선언은 다음과 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
// @Input params
// const Scene scene : Scene pointer.
// const Point3f &hitpoint : Point that will be rendered. Must be represented in world coordinate.
// const Point3f &light_pos : Sampled position on Emitter. Must be represented in world coordinate.
// Normal3f &light_normal : Normal vector on `light_pos`. Must be represented in world coordinate.
//
// @Output params
// Sampler *sampler : Sampler pointer.
// float pdfDir : Probability that `light_pos`->`hitpoint` direction is sampled.
//
// @return : Radiance emitted from light_pos to `hitpoint`.
virtual Color3f Sample_Le(
const Scene *scene,
const Point3f &hitpoint,
const Point3f &light_pos,
const Normal3f &light_normal,
Sampler *sampler,
float &pdfDir) const = 0;
|
cs |
(2019-07-18 수정 : sampler는 굳이 있을 필요가 없는것 같다)
PBRT는 Sample_Le() 안에서 광원에서의 법선 벡터도 계산하지만, 우리는 앞서 구현한 Mesh::samplePosition() 이 그 기능을 수행하기에 light_normal을 상수 입력으로 넘겼다.
이 인터페이스를 구현하는 AreaLight를 구현해보자. AreaLight의 생성자는 위에서 구현했으니, Sample_Le()를 구현하면 된다.
구현하기 전에, 내가 자료를 찾아봐도 Diffuse 관련한 설명밖에 나오지 않아서, 나는 이 AreaLight를 Diffuse Area Light로 가정하고 구현했다. 무엇보다 PBRT에서도 그렇게 돼있음...
역시 PBRT를 많이 참고했다(링크). hitpoint와 light_pos가 주어진 이상 빛의 방향도 주어진 것이나 다름없고, 함수에서 할 일은 light_pos에서 hitpoint로 radiance가 도달할 수 있는지를 확인하고, 그 방향이 sampling 될 확률을 구하는 것이다.
전체 Sample_Le() 코드는 다음과 같다.
Diffuse Area Light의 특징 중 하나가, 빛의 방향을 샘플링하면 Warp::squareToCosineHemisphere()를 따른다는 것이다. 반환하는 값이 항상 m_radiance인 것도 Diffuse의 특징이라고 하는데, 사실 잘 이해가 안간다...
기존에 없던 Emitter 인터페이스를 구성하고, 그 인터페이스를 다른 코드에서 사용할 수 있게 하기 위해 여러 파일에 자잘한 수정을 해야했다. 커밋을 참고하시라.
이제 whitted.cpp를 보자. Integrator 인터페이스는 렌더링을 시작하기 전에 미리 필요한 작업을 할 수 있도록 preprocess()를 제공한다.
최소한의 수정을 하려고 했더니 Emitter에 접근하려면 Scene 안에 있는 Mesh를 통해야만 했다. preprocess()에선 미리 Emitter를 가진 Mesh를 따로 모아 WhittedIntegrator의 멤버 변수에 저장한다.
Scene 안에 광원이 하나만 있다는 보장이 없다. 당장 테스트 파일에도 AreaLight가 두 개다. 많은 광원 중 하나를 선택하기 위해서, preprocess()에서 m_emitter_dpdf를 구성한다. 1.0f를 넣은 이유는 딱히 없고, 모든 광원을 uniform하게 뽑기 위해서다(uniform하게 뽑는 것이 좋은 방법인지는 모르겠다).
이제 Li()를 구현해보자. 우선 카메라에서 나온 광선이 주어진 Scene에 충돌하는지 검사한다. 충돌하지 않으면 당연히 검은색을 반환한다.
이제 광원을 선택해보자. 앞서 구성한 m_emitter_dpdf를 이용해 index를 뽑고, 그 index에 있는 광원을 사용하게 했다. Li()의 파라미터가 sampler이므로, 굳이 샘플을 재사용할 필요가 없어 sample() 함수를 사용했다.
이제 앞에서 구현한 samplePosition()을 이용해 광원 위의 점을 sampling했다.
위에서 선택한 Emitter의 Sample_Le()를 이용해 광원 위의 점에서 hitpoint로 향하는 radiance를 구했다.
Sample_Le()를 앞서 구현했지만, 이 안에서 hitpoint와 광원 위의 점이 서로에게 보이는지 등을 체크한다. 즉 Sample_Le()의 결과가 Color3f(0.0f)과 같다면 이어지는 계산을 할 필요가 없이 바로 Color3f(0.0f)를 반환한다.
이제 fr 항을 구한다.
BSDF::eval()은 BSDFQueryRecord를 입력으로 받는다. BSDFQueryRecord를 적절히 생성해 eval()에 넣으면 된다. 미리 구현되어 있어 편리했다.
이제 Geometry term을 계산한다.

V()는 visibility function이다. x와 y가 서로에게 보이면 1, 아니면 0이다. 방금 전 코드에서 체크했으므로, 이 시점에서 V()는 1이라고 가정했다.
분자의 nx는 x에서의 노멀 벡터, x->y는 x에서 y로 향하는 벡터이다. 반대도 마찬가지다. 분모는 x와 y 사이의 거리의 제곱이다. 구현할 때 x와 y는 sampling한 광원 위의 점과 hitpoint가 된다.
당연하지만 중요한 것은, 각 항을 같은 좌표계에서 계산했다는 것이다. hitpoint_to_light, light_normal, light_pos 는 world coordinate로 표현됐기 때문에 별 다른 변환을 하지 않고도 a와 c를 구할 수 있었다.
광원 위의 점에서의 노멀 벡터는 우리가 위에서 구했지만, hitpoint에서의 노멀 벡터는 Intersection 안의 Frame::cosTheta()로 구해야한다. cosTheta()의 파라미터는 local coordinate 상의 벡터를 필요로 하기 때문에 world coordinate의 hitpoint_to_light를 변환해 사용했다.
이제 세 항을 모두 구했으니 모두 곱하면 된다. 하지만 우리가 풀려고 하는 것은 적분식이고, 대수적으로 풀 수 없기 때문에 몬테카를로 적분을 이용해야 하는 것을 잊지 말자. 먼저 광원 위의 점이 나올 확률로 나눠야 하고, 그리고 선택한 광원이 나올 확률로 나눠야 한다. light_dir_pdf로는 나누지 않은 이유는 이미 light_pos를 뽑음으로써 빛의 방향이 정해졌기 때문이다.
전체 whitted.cpp 코드는 다음과 같다.
나머지는 다음 포스팅에 올리려고 한다.
링크
나중에 수정이 될 수도 있으니 최신 코드도 참고하기




