[Nori] Assignment 3: MC sampling과 Ambient Occlusion

--- 2021/6/25 수정 : 코드 관련 부분 삭제

이번 Assignment는 warp.cpp의 함수들을 구현하고 두 가지 간단한 렌더링 알고리즘을 다룬다.

 

Part 1. Monte Carlo Sampling

 

 렌더링을 할 때 2d Point를 여러가지로 변환하는 경우가 많다. 여기서는 squareToTent, squareToUniformDisk, squareToUniformSphere, squareToHemiSphere, squareToCosineHemisphere, squareToBeckmann과 각각의 PDF를 구현한다.

 

1.1 squareToTent

 

2d Point를 Tent Distribution으로 mapping하는 함수이다. Tent Distribution은 다음과 같이 나타난다.

 

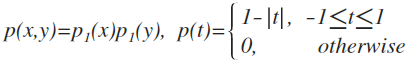
이 Probability Density Function(PDF) 를 따라 sampling 하기 위해서 Cumulative Density Function(CDF)를 구하고 역함수를 취한다. CDF는 PDF를 적분해 얻을 수 있다.

역함수를 취하면,

 

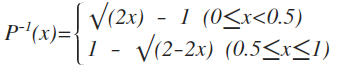
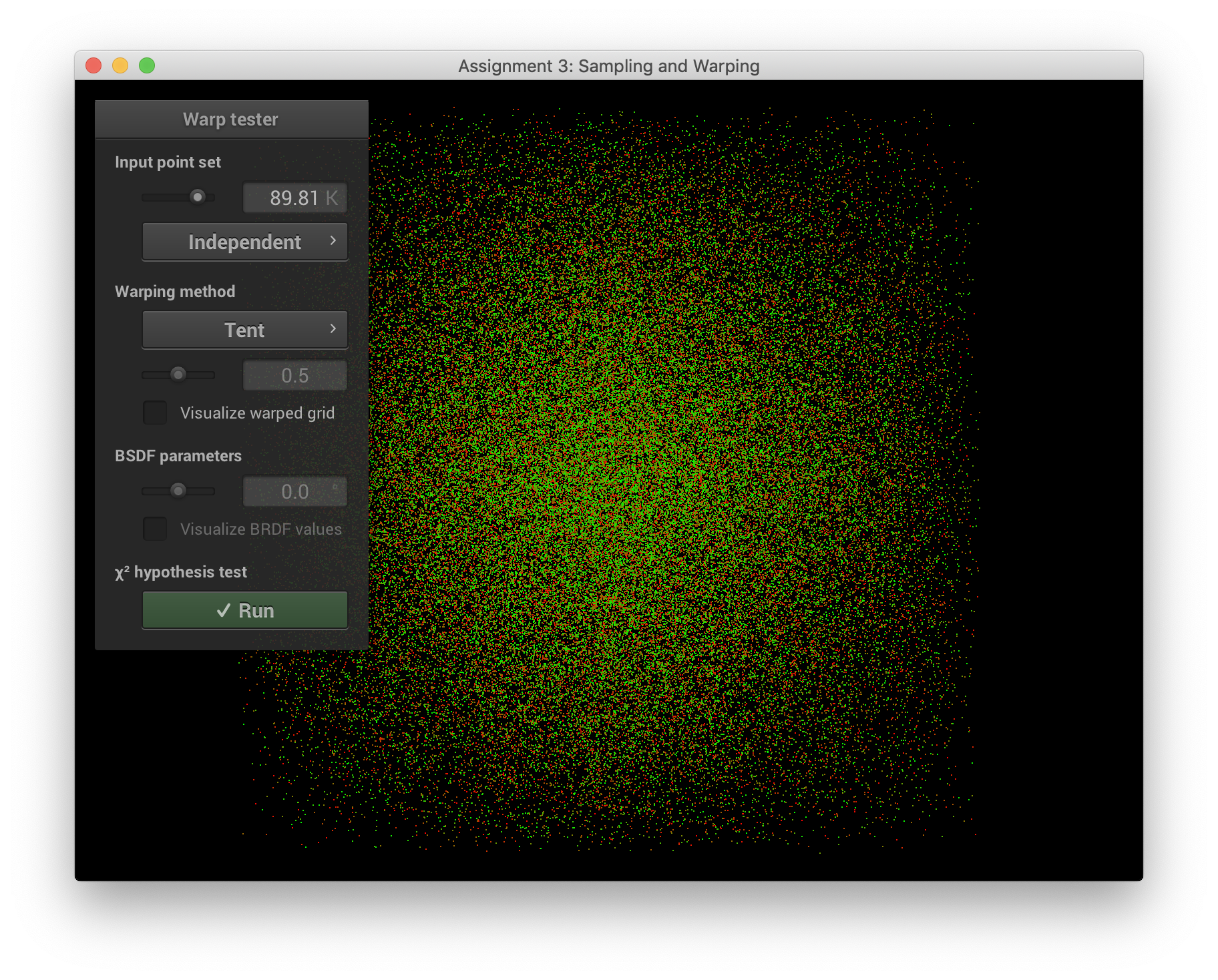
squareToTentPdf()는 주어진 식과 같다.

1.2 squareToUniformDisk

 

이번에는 2d Point를 단위원 위의 한 점으로 mapping하는 함수다. 원 위의 한 점은 (r * cos(Θ), r * sin(Θ)) 로 나타낼 수 있다. r = x, Θ = 2 * point[1] 로 바꾸면 저 식은 2d Point를 원으로 mapping하는 함수가 된다.

Point2f Warp::squareToUniformDisk(const Point2f &sample) {
    float rad = sample[0];
    float angle = sample[1] * M_PI_DOUBLE;
    return Point2f(rad * cos(angle), rad * sin(angle));
}

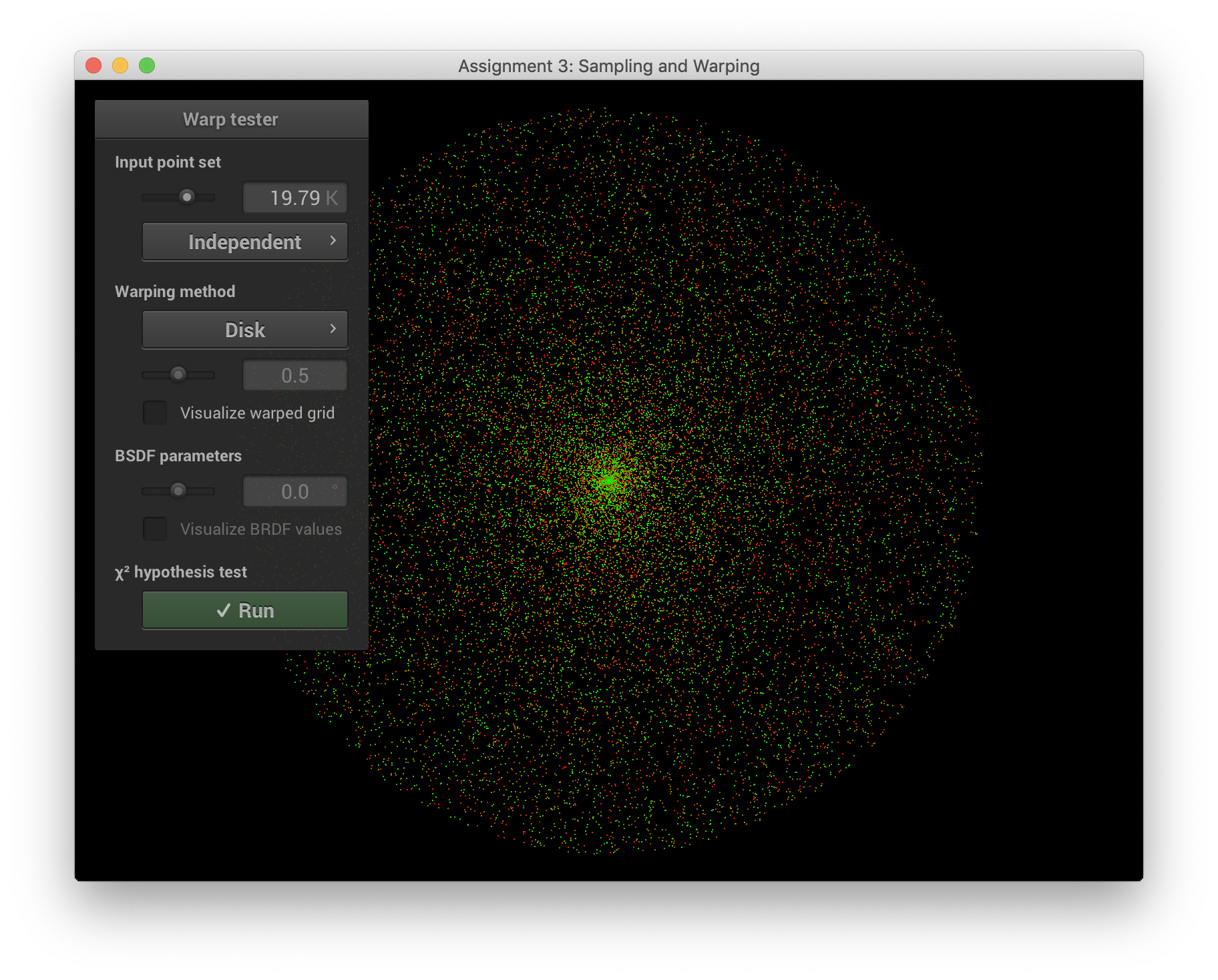
하지만 위의 함수로부터 분포된 점을 보면 Uniform 과는 거리가 먼 것을 확인할 수 있다. 왜냐하면 반지름을 uniform하게 sampling했기 때문이다.

 

 

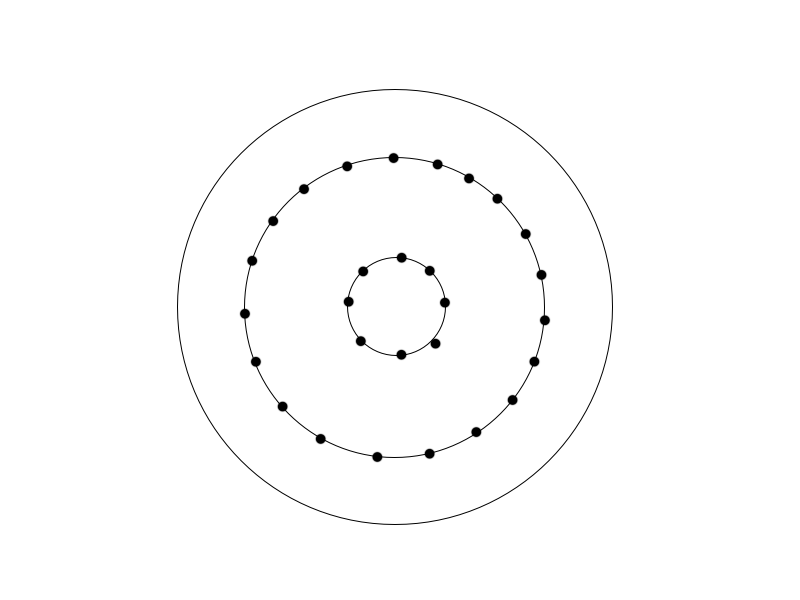
원 안의 점이 uniform하게 sampling 된다는 것은 r 거리의 원 위에 같은 수의 점이 있는것으로 생각할 수 있다. 예를 들어 r = 0.3 에 점이 10개 있다면, r = 0.6에 점이 20개 있어야 uniform하게 된다. 즉 반지름 r이 뽑힐 확률은 2πr , 상수를 없애면 r에 비례함을 알 수 있다. 따라서 반지름에 대한 PDF은

 

normalized PDF : y = 2x

 

이 됨을 알 수 있다. PDF를 이용해 위의 squareToTent와 같은 방법으로 반지름을 sampling할 수 있다.

 

CDF : y = x^2

inverse of CDF : y = √x

 

CDF의 역함수의 함숫값을 이용해서

 

(√r * cos(Θ), √r * sin(Θ))

 

이 uniform한 점의 좌표가 됨을 알 수 있다.

 

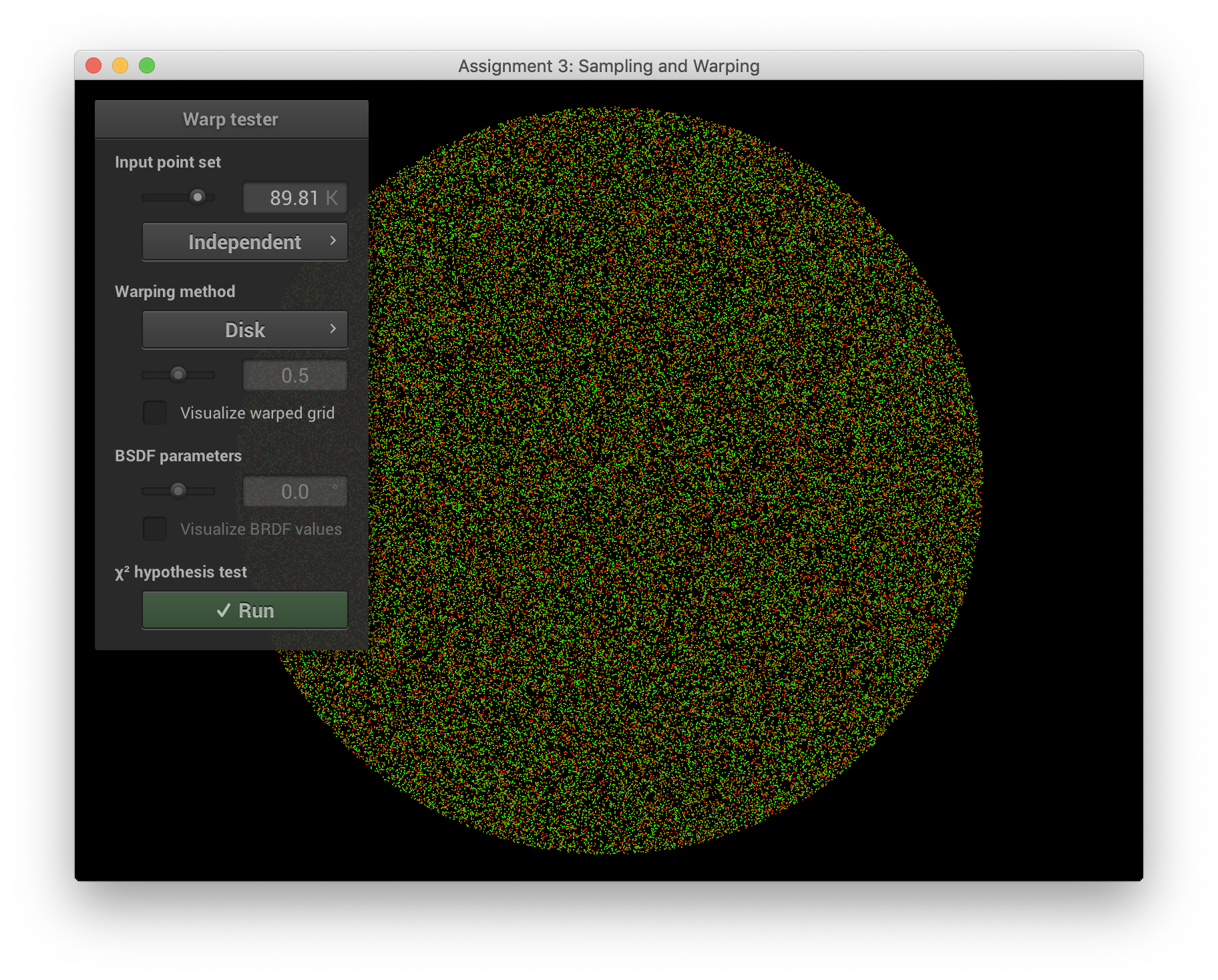
squareToUniformDiskPDF()는 1 / (원의 넓이)이다. 원점과의 거리가 0보다 큰 경우는 0을 반환한다.

 

1.3 squareToUniformSphere

 

2d Point를 단위구 위의 한 점으로 mapping하는 함수다. 반지름이 1인 구 위의 한 점은 구면좌표계를 이용해 구할 수 있다.

 

 

φ = 2π * x : [0, 2π)

Θ = π * y : [0, π)

(sin(Θ) * cos(φ), sin(Θ) * sin(φ), cos(Θ))

 

squareToUniformDisk와 같은 방법으로 접근하면 Θ가 뽑힐 확률은 2π * sin(Θ)에 비례한다. 즉 Θ에 대한 PDF는

 

normalized PDF : y = sin(x) / 2

CDF : y = (-cos(x) + 1) / 2

inverse of CDF : y = acos(1 - 2x)

 

Uniform하게 sampling한 구의 표면의 점의 좌표는

 

φ = 2πx : [0, 2π)

Θ = acos(1 - 2y) : [0, π)

(sin(Θ) * cos(φ), sin(Θ) * sin(φ), cos(Θ))

 

가 됨을 알 수 있다.

 

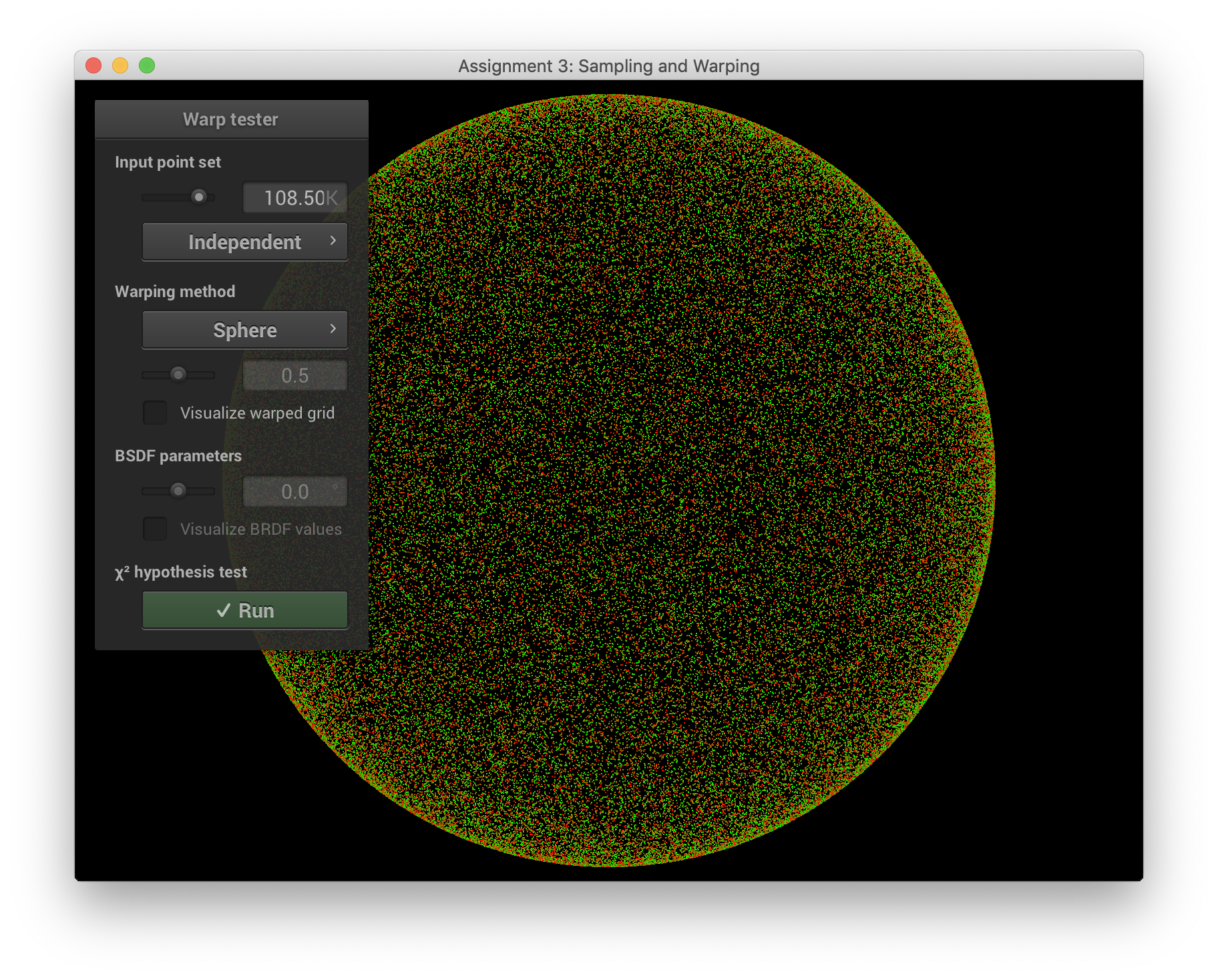
squareToUniformSpherePDF()는 1 / (구 표면의 넓이) 이다.

 

1.4 squareToUniformHemiSphere

 

단위구를 자른 반구로 mapping하는 함수이다. squareToUniformSphere와 유사하지만 Θ가 [0, π/2]인 점이 다르다. 

 

normalized PDF : y = sin(x)

CDF : y = 1 - cos(x)

inverse of CDF : y = acos(1 - x)

 

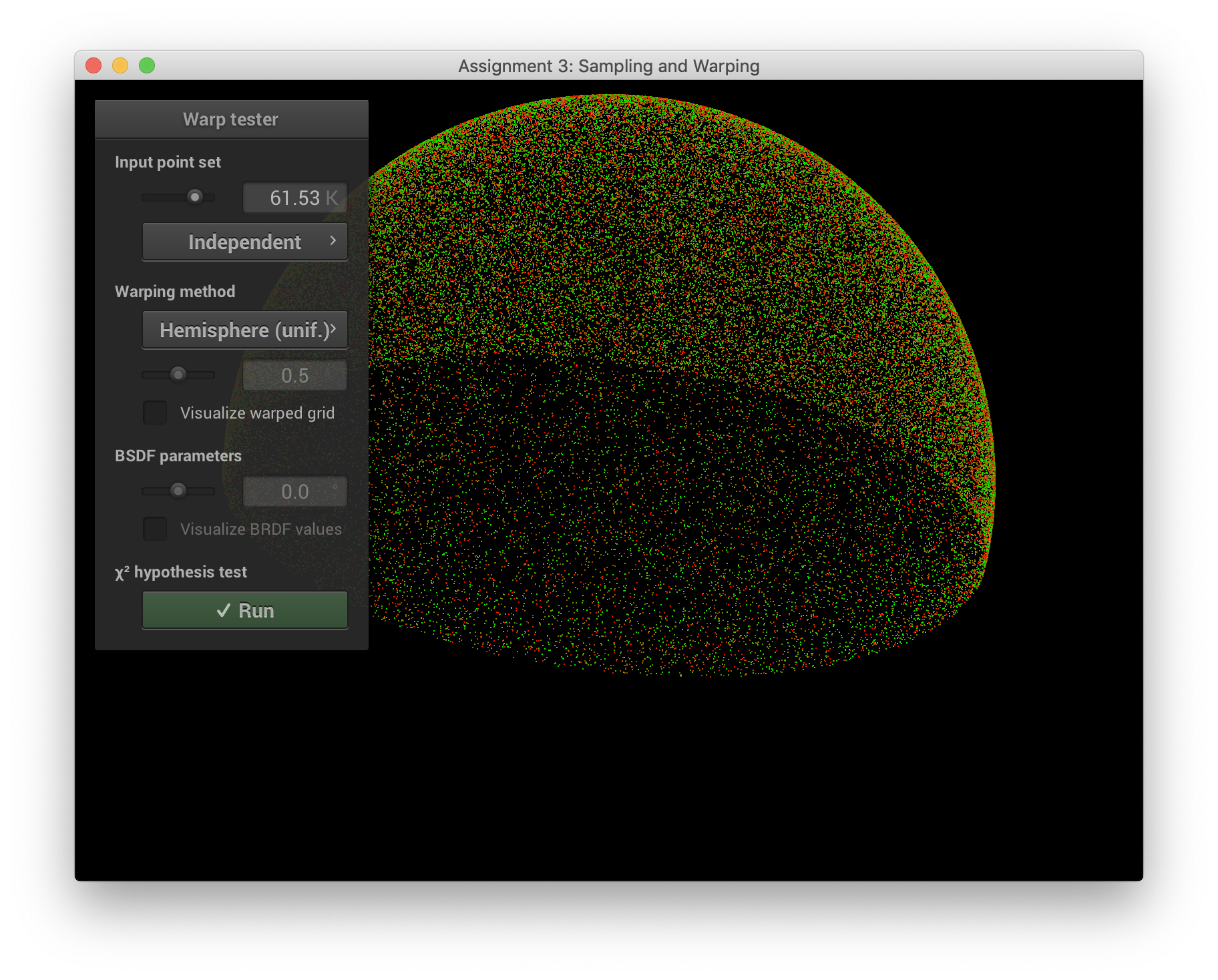
squareToUniformHemiSpherePdf()는 1 / (반구 표면의 넓이) 이다.  Z 좌표가 0보다 작은 경우는 0을 반환한다.

 

1.5 squareToCosineHemisphere

 

이번에는 반구 위로 Uniform하지 않고 Cosine-weighted 하게 mapping하는 함수이다. 즉, PDF는 다음과 같다.

 

 

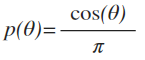
이 때 Θ는 북쪽으로 뻗는 축과 반구 위의 점 사이의 거리이다. 이렇게 sampling 하는 효율적인 방법이 있다.

 

 

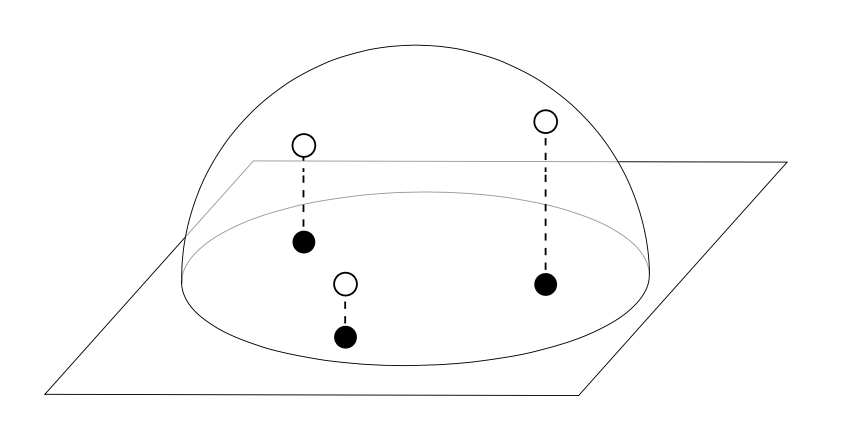
그림과 같이 밑 면의 원을 Uniform하게 sampling한 점을 반구로 투영시키면 우리가 원하는 Cosine-weighted하게 sampling이 된다고 한다.

squareToCosineHemispherePdf()는 주어진 식을 그대로 구현한다. 반구인 경우이므로 z 좌표가 음수일 확률은 0이다.

 

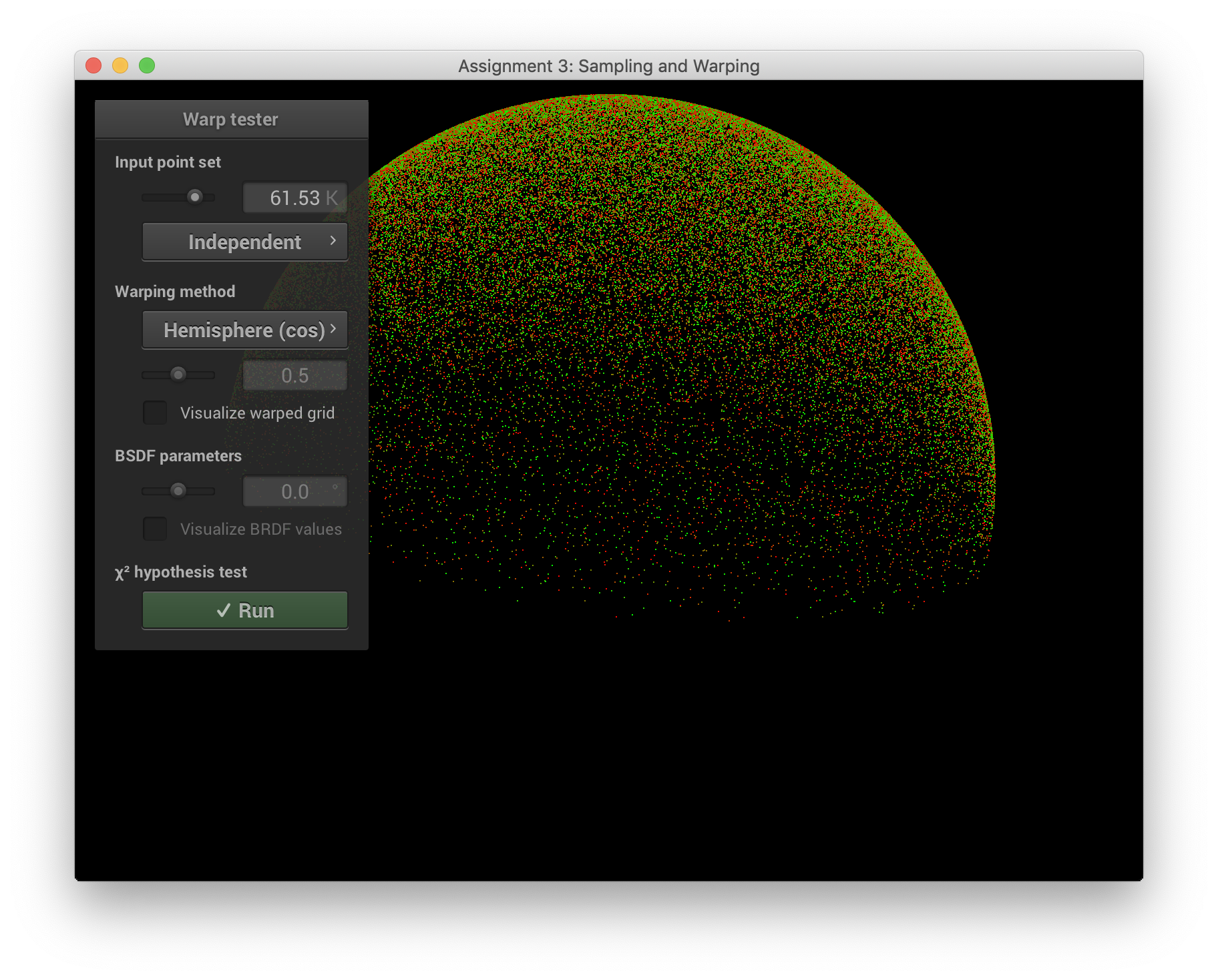
squareToUniformHemisphere()와 비교해보면 밑면의 둘레 부분에 점이 조금 찍힌걸 확인할 수 있다.

 

1.6 squareToBeckmann

 

(2019.4.2 수정) nori-old에는 이 단계가 5번째 Assignment에 나온다.

 

이번에는 Beckmann distribution을 구현해본다. PDF는 주어진 것을 그대로 구현하면 된다. PDF는 다음과 같다.

 

 

φ는 2 * π * x로 균일하게 sampling하면 된다. Θ는 위와 같은 방법으로 PDF를 적분하고 역함수를 취해 sampling을 할 수 있다.

 

 

이해가 안가는게, 적분을 하는데 Assignment에 나온 것 처럼 sin(Θ)를 곱해 적분해야 했다. 

 

 

 

 

 

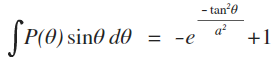
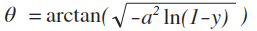
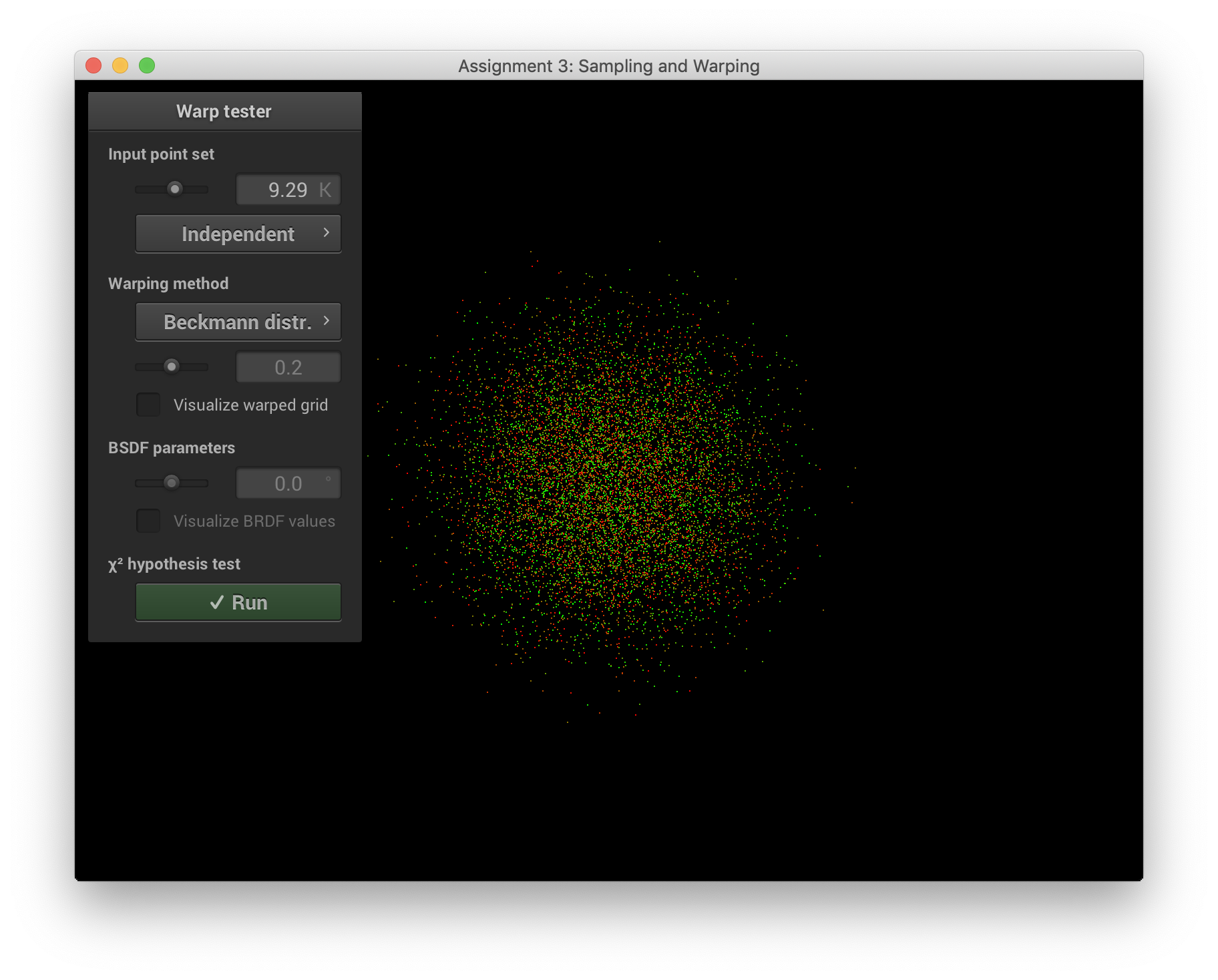
Part 2. Two simple rendering algorithms 

 

2.1 Point lights

 

이번엔 Point Light를 나타내는 SimpleIntegrator를 구현한다. Point Light는 전처리 과정이 필요없으므로 사실 Integrator 인터페이스의 Li() 함수를 구현하는 일과 같다. Li()는 scene, sampler, ray를 파라미터로 갖는다. 주어진 ray를 추적해 scene과의 충돌 지점의 radiance를 반환한다.

 

다음은 SimpleIntegrator를 사용하는 Scene xml 파일의 일부이다.

 

<integrator type="simple">
    <point name="position" value="-20, 40, 20"/>
    <color name="energy" value="3.76e4, 3.76e4, 3.76e4"/>
</integrator>

 

Point Light의 좌표와 세기를 나타내는 position, energy 파라미터를 갖는다. SimpleIntegrator의 생성자에 두 파라미터를 받는다.

 

SimpleIntegrator(const PropertyList &props) {
    m_position = props.getPoint("position");
    m_energy = props.getColor("energy");
}

 

SimpleIntegrator의 Li()는 다음을 계산해야 한다.

 

 

Φ는 파라미터로 주어진 energy, p는 Point Light의 위치, x는 렌더링이 되는 점이다. 이 x는 ray가 scene에 충돌하는 점이다. Θ는 x에서 p로 향하는 벡터와 x에서의 노멀 벡터 사이의 각이다. 마지막의 생소한 항은 visibility function인데, 다음과 같이 정의된다.

 

 

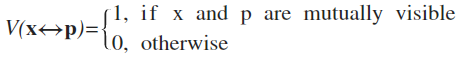
즉 x에 광원의 빛이 닿지 않으면 0, 그렇지 않으면 1이다. 이는 충돌점에서 광원으로 향하는 shadow ray를 만들어 충돌시켜 알 수 있다.

이를 구현한 전체 Li() 코드는 다음과 같다.

구현하면서 어려웠던 점은 함수의 반환 값이 World coordinate인지 Local coordinate인지 구분하는 것이었다. 사용하진 않았지만, its.shFrame.n, its.p 는 World coordinate이다. its.shFrame.toLocal()는 충돌점의 Local coordinate로 변환한다. 이 좌표계의 법선 벡터는 (0,0,1)이므로, 변환된 벡터를 normalize한 것의 z 값이 곧 cos_theta가 된다.

2.2 Ambient occlusion

 

이번엔 Ambient occlusion를 나타내는 AOIntegrator를 구현한다. Point Light와 같이 Ambient occlusion도 전처리 과정이 필요없으므로 사실 Integrator 인터페이스의 Li() 함수를 구현하면 된다.

AO는 별다른 파라미터를 받지 않는다. 따라서 AOIntegrator의 생성자는 따로 구현할게 없다.

AOIntegrator는 다음을 계산하면 된다.

 

 

x는 렌더링될 점, ω는 들어오는 빛의 방향, Θ는 x에서의 노멀 벡터와 ω 사이의 각도, α는 빛이 나아갈 수 있는 최대 거리이다. 문제에서는 (α = ∞) 로 가정하였다. 즉 전역 조명을 가정한다. V는 Point Light에서와 같은 visibility function이다. 즉 빛이 무언가에 가리면 0, 그렇지 않으면 1이다. 

 

L(x)를 적분해서 계산하기 위해 몬테카를로 적분(MC Integration)을 사용하였다. 확률을 이용해 적분하기 어려운 함수를 적분하는 건데, 결론만 말하자면 다음을 계산하면 된다.

(2019-07-02 추가) 블로그에 몬테카를로 적분에 관한 포스팅을 작성했다.

 

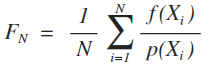
구현한 Li() 코드는 아래와 같다.

바로 위의 식에서 N이 SAMPLE_NUM으로 구현되었다. 

 

SAMPLE_NUM = 1 (13.9 min)

 

SAMPLE_NUM = 5 (31.3 min)

링크

나중에 수정이 될 수도 있으니 최신 코드도 참고하기

MC sampling 커밋

 

SimpleIntegrator 커밋

 

AOIntegrator 커밋

 

Assignment 3

 

(2019-01-23에 작성됨)