--- 2021/6/25 수정 : 코드 관련 부분 삭제
이번 Assignment에서는 새로운 Integrator인 Path Tracer와 불투명한 재질을 나타내는 Microfacet Model, 그리고 multiple importance sampling을 이용한 path tracer를 구현해본다. 특히 이번 포스팅에서는 Microfacet Model을 구현할 것이다.
시작하기 전에, 내가 이때까지 진행했던 자료는 nori가 아니라 nori-old이다. 물론 최근 자료(nori)로 진행하면 좋지만, 실제로 수업에 쓰이는 자료이다 보니 모든 Assignment를 볼 수 없었고 매 학기마다 천천히 공개가 되기 때문에 nori-old로 진행했었다. 그런데 nori-old와 nori의 진행 순서나 내용이 조금 다른것을 최근에 발견했다. 2번 Assignment는 nori, 3~4 Assignment는 nori-old로 진행했었는데, 이번에는 nori-old로 진행하되 nori에 추가되거나 중복되는 내용들을 추가하거나 뺄것이다.
nori : https://wjakob.github.io/nori
nori-old : https://wjakob.github.io/nori-old
1. Mircofacet BRDF
1.1 Evaluating the Beckmann distribution (nori-old)
1.2 Sampling the Beckmann distribution (nori-old)
이전 포스팅 참고
1.3 Evaluating the Microfacet BRDF
반사, 투과를 기하광학(geometric optics)적으로 접근하는 것은 거친 표면을 미세한 작은 표면들로 이루어져 있다고 생각하는 것에 기반한다고 한다. 사실 이 문장은 pbrt에 있는 문장에 번역기의 힘을 조금 빌렸는데, 나는 이번에 기하광학이라는 말을 처음 들었다. 빛이 진행할 때 나타나는 특징들을 연구하는 분야라고 하는데, 여튼 거친 표면을 여러개의 작은 표면으로 구성하면 뭔가 좋겠지.. 하고 넘어가자.
이런 미세한 작은 표면들이 어떻게 분포했는지에 따라 표면이 얼마나 거친지, 혹은 매끄러운지를 나타낼 수 있다.
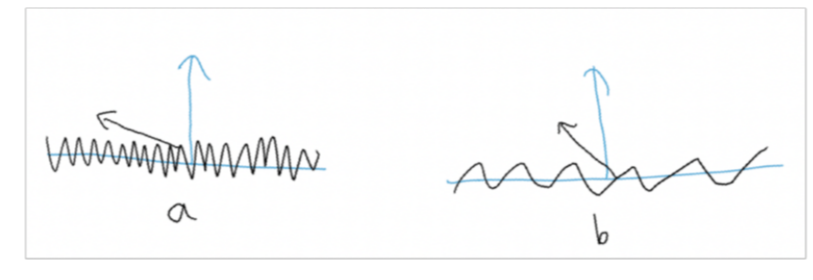
b 표면보다 a 표면이 더 거칠다고 직관적으로 이해할 수 있는데, 이를 수학적으로 각각의 극소면의 노멀 벡터의 분포로 나타낼 수 있다. 즉 전체적인 노멀 벡터에 비해서 이루는 각도가 큰 노멀 벡터가 많으면 표면이 거칠고, 이루는 각도가 작은 노멀 벡터가 많으면 표면이 상대적으로 매끈하다고 할 수 있다고 이해했다.
이런 microfacet 모델을 이루는 두 가지 중요한 요소는 극소면의 분포를 나타내는 것, 그리고 각각의 극소면에서 빛이 어떻게 산란하는 지를 나타내는 BRDF이다. 극소면의 분포를 나타낼 때, 즉 극소면의 노멀 벡터의 분포를 나타낼 때 앞서 구현한 Beckmann distribution을 사용하려고 한다. BRDF의 경우에는 mirror에서 쓴 전반사를 microfacet의 specular 측면의 BRDF로, Oren-Nayer model을 diffuse 측면의 BRDF로 가장 많이 사용한다고 한다. 하지만 우리는 여기서 Oren-Nayer 대신 Lambertian BRDF를 사용할 것이다. microfacet의 전체 BRDF는 두 BRDF의 조합으로 나타난다.
앞에서 구현한 Dielectric과 다르게 Microfacet의 isDiffuse()는 true를 반환한다.
이제 빛이 들어오는 방향과 나가는 방향이 주어졌을때 brdf 값을 계산하는 eval(), 그리고 빛이 특정 방향에서 들어올 때 특정 방향으로 나갈 확률을 계산하는 pdf(), 그리고 빛을 specular로 처리할지 diffuse로 처리할지와 빛이 어디로 반사될지를 결정하는 sample()을 구현해보자.
eval()은 다음을 계산하면 된다.

kd, ks는 멤버변수 m_kd, m_ks로 각각 정의되어 있다. 내가 이해한 바로는, ks는 specular로 얼마나 반응하는 지를 나타내는 것 같고, kd는 diffuse로 작동할 때 빛을 얼마나 반사할 지를 나타내는 것 같다... 어디까지나 확실하지는 않다. wh는 wi와 wo를 더한 벡터를 normalize한 벡터이다. 의미적으로 이 때 wh는 microfacet의 극소면의 노멀 벡터를 나타낸다. F는 Dielectric을 구현할 때 살펴본 Fresnel reflectance이고, D는 앞에서 구현한 squareToBeckmannPDF()이고, G는 다음과 같이 정의된다.
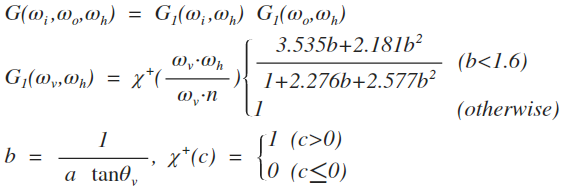
이를 차례대로 구현하면 eval()이 된다.
1.4 Sampling the Microfacet BRDF
이제 pdf(), sample() 을 구현해보자.
pdf()는 wi가 주어졌을 때 wo로 반사될 확률을 구한다. 문제에 주어진 density function을 구현하면 된다. D는 eval()과 마찬가지로 squareToBeckmannPDF()이다. 여기서 pdf()는 sample()에서 이미 wo를 sampling 한 것을 가정한다.
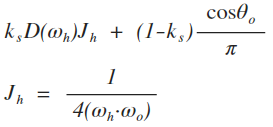
sample()에서 이제 입사광을 diffuse로 다룰지, specular로 다룰지를 결정한 후, 그에 맞는 wo를 sampling하면 된다. Nori에 적힌 설명을 옮겨보자면,
- uniform하게 뽑힌 변수 하나로 specular인지, diffuse인지 정한다.
- 이 때 사용한 랜덤 변수를 뒤에서 재사용하기 위해 조절한다.
- diffuse인 경우에, cosine-weighted 인 wo를 뽑는다.
- specular인 경우에, squareToBeckmann()을 이용해 극소면의 노멀 벡터를 뽑고, 전반사를 이용해 wo를 구한다.
이 과정에서 내가 이해가 가지 않았던 건 샘플을 재사용하는 방법이다. 알고보니 꽤 단순했는데, 쉬운 예를 들어보자.
[0.0, 1.0) 구간의 랜덤 변수 s 하나로 두 가지 일을 하고 싶다고 가정하자. 이 두 일은 독립적이기에, 당연히 원래대로라면 두 개의 랜덤 변수가 필요하다.
- s의 구간을 나눈다. [0.0, 0.5) [0.5, 1.0)
- 만약 s가 [0.0, 0.5) 구간에 있으면, 랜덤 비트를 0으로 설정하고, s에 2를 곱해 [0.0, 1.0) 구간에 있게 한다.
- s가 [0.5, 1.0) 구간에 있으면, 랜덤 비트를 1로 설정하고, s를 조절해 (0.0, 1.0) 구간에 있게 한다. (s' = (s - 0.5) / 2)
즉 float의 정확성을 조금 포기하더라도, 하나의 랜덤 변수로 두 가지의 일을 할 수 있다. 두 부분 구간 중 어느 쪽에 들어갈 지를 비트 한개로 결정하고, 나머지를 이용해 두 번째 일을 하는 것이다. 그림으로 표현하면 다음과 같다.

당연하게도 여기서 실수하지 말아야 하는 것은 비트를 겹쳐서 쓰지 않는 것이다.
전체 microfacet.cpp 코드는 아래와 같다.
(파싱이 제대로 안된다. 밑에 링크에서 보는게 더 편할듯)


링크
나중에 수정이 될 수도 있으니 최신 코드도 참고하기
'Dev > Computer Graphics' 카테고리의 다른 글
| [Nori] Assignment 5: Path Tracing, Microfacet Models, and Multiple Importance Sampling #2 (0) | 2019.07.04 |
|---|---|
| [Nori] Assignment 4: Distribution과 Whitted-style Ray Tracing #2 (0) | 2019.04.01 |
| [Nori] Assignment 4: Distribution과 Whitted-style Ray Tracing #1 (0) | 2019.02.15 |
| [Nori] Assignment 3: MC sampling과 Ambient Occlusion (0) | 2019.02.15 |
| [Nori] Assignment 2: Octree 만들기 (0) | 2019.02.15 |



