이번 포스팅의 주제는 Nori assignment 3에서 쓱 지나쳤던 몬테카를로 적분이다. 며칠 전부터 TU Wien에서 올라온 Rendering/Ray Tracing 강의를 보고 있는데, 여기 교수님이 말씀하시기를, 이 이론은 정말 정말로 중요하고, 잘 기억은 안 나지만 중요한 수학 이론 10개를 꼽으라면 항상 손가락 안에 든다고 하셨다. 나도 확실하게 잘 알던 내용도 아니라서, 내가 이해한 나름대로 정리하려고 한다.
살짝 TMI 같지만 이 이론은 맨해튼 프로젝트를 진행할 때 복잡한 적분식을 풀려고 고안되었다고 한다. 여기서 말하는 적분식은 어떤 종류를 말하는 걸까? 적분식을 닫힌 형태(closed-form)로 풀 수 없을 때 쓴다고 하는데, 적당히 풀기 어려운 식으로 이해했다.
그래픽스를 공부하는 입장에서, 몬테카를로 적분은 Rendering Equation을 풀 때 많이 사용한다.

이런 복잡한 적분식을 풀 때 몬테카를로 적분을 사용해 적분 값을 추측할 수 있다.

1. 기댓값
기댓값은 어떤 사건에 대해 확률 변수와 그 확률 변수가 나올 확률을 곱한 것을 모두 더한 값이다. 다르게 말하면, 어떤 사건의 평균값? 이라고도 할 수 있다. 모르는 사람이 없는 예시를 들어보자.
주사위를 15번 반복해서 던졌을 때 나온 눈의 평균값은 얼마일까? 이를 구하는 방법 중 가장 단순한 방법은 직접 해보는 것이 아닐까?

하지만 아까 던진 15번의 평균값과 지금 던진 15번의 평균값은 다를 확률이 매우 크다. 그리고, 누가 만약 1000번에 대해 물어보면 뭐라고 답할까? 1000번을 직접 던져보기에는 시간이 아깝다. 하지만 저 질문에 대해 3.5라고 대답한다면 꽤 그럴싸하다. 왜냐하면 주사위를 던지는 사건에 대한 기댓값은 3.5이기 때문이다.
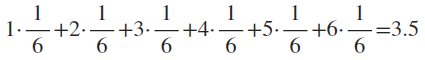
기댓값이 3.5라는 것은, 주사위를 던지면 던질수록 나오는 눈의 평균값은 3.5에 점점 수렴한다는 뜻이다.
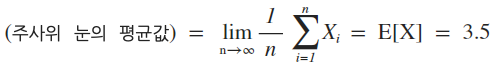
위의 주사위의 경우는 확률 변수가 이산적인 경우이다. 앞에서 확률 변수의 값과 그 값이 나올 확률을 곱한 것을 모두 더한 값이라고 했다.
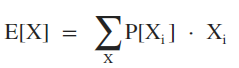
확률 변수가 연속적인 경우도 있다. 모든 확률변수에 대해 시그마 대신 적분을 취한다.

2. MC 적분
이제 기댓값을 이용해 MC적분을 알아보자.

확률 변수 x는 a와 b 사이에서 sampling 될 것이고, x가 특정 값으로 sampling 될 확률을 p(x)라고 하자. 우리는 위 적분식을 아래처럼 변형시킬 수 있다.

변형된 식을 가만히 놓고 보면, f(x)/p(x)의 기댓값을 구하는 식임을 알 수 있다.

우리가 구하려고 하는 적분 식이 'f(x) / p(x)'의 기댓값으로 나타난다는 것은, 풀기 어려웠던 원래의 적분식의 값을 여러 번의 시행만으로 그 값을 유추할 수 있다는 말이다.

3. 간단한 구현

import random
import math
def func(x):
return math.sin(math.tan(math.sin(math.cos(x))))
# Assume x is sampled uniformly
def pdf(lower, upper):
return 1.0 / (upper - lower)
sum = 0.0
log = 1
lower = 0.0
upper = 2.0
for i in range(1, 10000001):
rand = random.random() * (upper - lower) + lower
sum += func(rand) / pdf(lower, upper)
if log == math.log10(i):
print("sample " + str(i) + " numbers, result : " + str(sum/i))
log += 1
sample 10 numbers, result : 0.467712314634
sample 100 numbers, result : 0.777210424726
sample 1000 numbers, result : 0.850172274937
sample 10000 numbers, result : 0.857423348551
sample 100000 numbers, result : 0.852955833775
sample 1000000 numbers, result : 0.854691950966
sample 10000000 numbers, result : 0.85500621829점점 수렴하는 모습을 보인다.
'Dev > Theory' 카테고리의 다른 글
| 렌더링 방정식 (Rendering Equation) (0) | 2019.07.03 |
|---|---|
| 재질을 표현하는 방법 : BRDF, BTDF, BSDF (0) | 2019.06.27 |
| 빛이 다른 매질로 갈 때 : 스넬의 법칙, 프레넬 계수 (Snell's Law, Fresnel Coefficient) (0) | 2019.03.12 |
| 밝기를 측정하는 방법 : Radiant Flux, Irradiance, Radiant exitance, Radiance (0) | 2019.02.22 |



