(BSDF 포스팅에서 이어짐)
Rendering Equation은 요즘 쓰이는 거의 모든 렌더러가 기본으로 하는 이론이다. 렌더링을 한다는 것은 곧 이 방정식을 푼다는 것과 같고, 여러 가지 렌더링 알고리즘들은 대부분 이 방정식을 얼마나 빠르고 효율적으로 풀 수 있는지에 그 초점을 둔다.
Scene 안의 어떤 물체의 표면에 있는 점 x, 그리고 x를 보고있는 카메라를 생각해보자. 광원에서 출발한 빛은 Scene안에서 반사되고 투과되면서 우연히 점 x로 향할 것이다. 어떤 빛은 어떤 경로를 통해서 x로 오고, 다른 빛은 다른 경로를 통할 것이고, 그 경로의 경우의 수는 무수히 많을 것이다.

하지만 결국 x를 보고 있는 카메라는 x로 들어오는 빛을 보는게 아니라, x에서 카메라 방향으로 반사된 빛만을 볼 것이다.

하지만 전구나 태양같이, 어떤 물체는 스스로 빛을 내기도 한다. 점 x가 광원이라면, 카메라가 x를 볼 때 광원에서 카메라로 향하는 빛도 볼 것이다.

즉, 카메라가 점 x를 볼 때 보는 빛은
카메라에서 x 방향으로 보는 빛 = x가 카메라 방향으로 스스로 내는 빛 + x에서 카메라 방향으로 반사되는 빛
이다. 이것이 렌더링 방정식의 의미이고, 이를 수식으로 나타내면 아래와 같다.
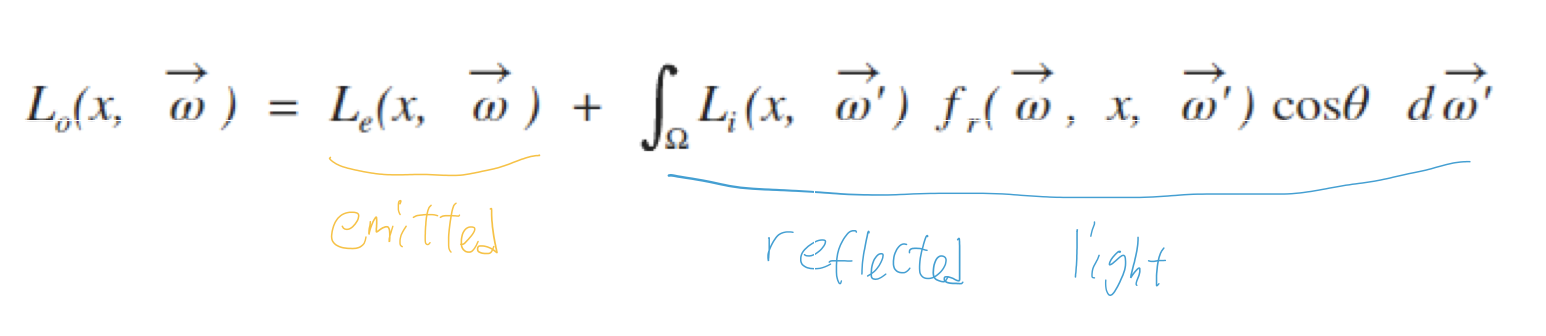
이 식은 Scene 안의 한 점 x에 적용되는 식이다. 실제로는 Scene 안의 모든 점에 대해 위의 방정식을 계산해야 한다. 빛을 시뮬레이션 할 때 우리가 주로 쓰는 단위는 Radiance이다. 물론 위 방정식에서도 Radiance를 사용한다. 식이 좀 헷갈릴 수 있는게, Lo(x, w), Le(x, w)랑 Li(x, w')의 빛의 방향이 다르다. Lo, Le는 x에서 w 방향으로 나가는거고, Li(x, w')는 w'방향으로부터 x로 들어오는거다. 식의 의미를 생각해보면 금방 이해할 수 있을 것이다.
w는 x에서 카메라로 향하는 방향, w'는 x로 향하는 어떤 방향이다. Lo는 x에서 카메라로 향하는 전체 Radiance이다. Le는 x에서 카메라로 나오는 Radiance이고, 그 뒤의 적분 부분은 임의의 방향 w'에서 x로 온 빛 중에서 w 방향으로 반사되는 빛의 Radiance의 모든 합을 의미한다.
척 보면 알겠지만 이 방정식은 closed form으로 정리가 불가능하다. 이 방정식을 제일 풀기 어렵게 만드는 요인은 적분 식이 재귀적이라는 것이다. 점 x에서 카메라로 가는 Radiance인 Lo는 주위 모든 점에 영향을 받는다. 하지만 점 x 또한 주위 모든 점에게 영향을 끼친다. 즉, integral 안에 있는 Li는 다른 점에서 x로 오는 Lo와 같고, Lo를 구하기 위해 다시 위 식을 적용해야 할 것이다.
이렇게 까다로운 적분식을 풀기 위해, 이 방정식을 제안한 Kajiya는 몬테카를로 적분을 이용한 Path Tracing 방식을 제안한다. 이 구현은 Nori Assignment 5에서 다룰 예정이다.
'Dev > Theory' 카테고리의 다른 글
| 재질을 표현하는 방법 : BRDF, BTDF, BSDF (0) | 2019.06.27 |
|---|---|
| 몬테카를로 적분 (Monte Carlo Integration, MC Integration) (0) | 2019.06.27 |
| 빛이 다른 매질로 갈 때 : 스넬의 법칙, 프레넬 계수 (Snell's Law, Fresnel Coefficient) (0) | 2019.03.12 |
| 밝기를 측정하는 방법 : Radiant Flux, Irradiance, Radiant exitance, Radiance (0) | 2019.02.22 |



