우리 주위의 물체들은 다양한 재질과 그에 따른 특성을 가지고 있다. 이를테면 우리는 투명한 물이나 유리 너머에 뭐가 있는지 볼 수 있지만 조금씩 다르게 보이고, 거울 너머를 볼 수 없지만 거울에 비치는 물체를 볼 수 있다. 금속은 내가 보는 방향에 따라 색이 밝아지기도 하고 상대적으로 어두워지기도 하지만, 천으로 만든 옷은 어떤 방향으로 봐도 색깔이 크게 달라지지 않는다.
재질마다 다르게 보이는 이유는 각 재질이 각기 다른 방식으로 빛을 반사하고, 다른 비율의 빛을 흡수하고, 그 나머지를 다른 방식으로 투과시키기 때문이다. 간단한 예시를 보자.

Specular는 정반사다. 들어오는 모든 입사광을 특정 반사각으로 반사시킨다. 거울이 이에 해당된다. Diffuse는 Specular와 대비되는 난반사다. 입사광을 모든 방향으로 고르게 반사시킨다. Spread는 Specular와 Diffuse의 특징을 모두 갖는다. 빛이 여러 방향으로 퍼지면서도 특정 방향으로 많이 반사된다.
이런 상호작용을 수학적으로 나타낼 수 있다. 컴퓨터 그래픽스에선 이런 물체와 빛이 상호작용하는 방식을 BRDF, BTDF, BSDF라는 함수로 정의한다. BRDF(Bidirectional reflectance distribution function)는 빛이 어떤 방향으로 반사가 되는지, BTDF(Bidirectional transmittance distribution function)는 빛이 어떤 방향으로 투과가 되는지, BSDF(Bidirectional scattering distribution function, 혹은 BxDF)는 이 둘을 합쳐 빛이 재질과 어떻게 상호작용하는지를 나타낸다. 이제 자세히 알아보자.
BRDF는 입사각 벡터, 표면 위의 점, 반사각 벡터를 파라미터로 받으면 주어진 반사각으로 반사될 확률을 리턴하는 함수이다. 다르게 말하면, 이 방향으로 들어온 빛이 그 방향으로 얼마나 반사될지를 나타낸다.

하지만 대부분의 재질은 빛을 조금이라도 흡수하고, 몇몇 재질들은 빛을 투과시키기도 한다. BRDF만으로 빛이 흡수하거나 투과하는 이 모든 현상을 표현할 수는 없다. 그래서 PBR에서는 BRDF 말고도 BTDF, BSDF가 필요한데, 이 포스팅에서는 BRDF를 중점적으로 보자.
BRDF의 특징
BRDF는 세 가지 중요한 특징이 있다.
1. Helmholtz-reciprocity
빛이 들어오는 방향과 반사되는 방향을 바꿔도 그 값이 같다.

2. Positivity
BRDF의 값은 항상 0 이상이다. 즉, 음수가 될 수 없다.

3. Energy conversion
세 번째 특징을 보기 전에, 간단한 개념 하나를 보자.

N벡터는 표면의 노멀 벡터, L벡터는 점에서 광원으로 향하는 벡터이다. 이 때, 햇빛이 90도의 각도로 점을 비추고 있을 때, 햇빛의 몇 퍼센트가 점으로 향할까? 이는 N벡터와 L벡터가 이루는 각에 따라 달라진다. 위의 경우는 N과 L 사이의 각이 0도이므로, 햇빛의 100퍼센트(cos0 = 1)가 점으로 비친다. 낮 12시에 제일 밝은 이유가 이것이다.
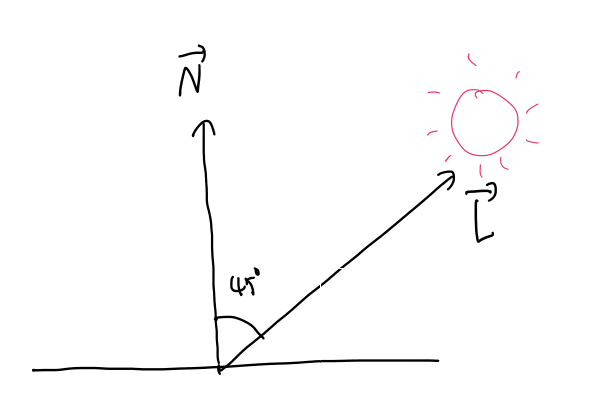
하지만 시간이 조금 지나 4~5시쯤에는 N벡터와 L벡터가 이루는 각이 점점 커진다. 이 때는 N과 L 사이의 각이 45도이므로, 햇빛의 약 70퍼센트(cos45 = 0.7)가 점으로 비춰진다. 태양이 지구로 보내는 에너지는 변함이 없지만, 지구에서는 햇빛을 받는 각도에 따라 그 양이 달라진다.
BRDF의 세 번째 특징은, 물체는 입사광을 반사하거나 흡수할 수 있지만, 들어오는 빛의 양보다 더 많은 양이 반사될 수 없다. 이를 식으로 표현하면 아래와 같다.
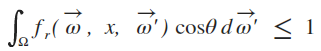
코사인이 붙은 이유는 위의 경우를 고려했기 때문이다.
적분값이 1이라면 모든 빛을 반사하는 재질인 경우이고, 1보다 작다면 빛의 일부를 흡수했기 때문이다. 1보다 큰 경우는 존재하지 않는다.
예시
좋은 예시는 아니지만, 이전 포스팅 에서 구현한 Microfacet이라는 재질의 BRDF를 구현한 코드를 보자(엄밀하게는 BSDF를 상속받지만, 빛이 투과하는 경우가 없다)
/// Evaluate the BRDF for the given pair of directions
Color3f eval(const BSDFQueryRecord &bRec) const {
// Copied from diffuse.cpp
if (bRec.measure != ESolidAngle
|| Frame::cosTheta(bRec.wi) <= 0
|| Frame::cosTheta(bRec.wo) <= 0)
return 0.0f;
const Vector3f w_h = (bRec.wi + bRec.wo).normalized();
const float D = Warp::squareToBeckmannPdf(w_h, m_alpha);
const float F = fresnel(w_h.dot(bRec.wi), m_extIOR, m_intIOR);
const float G = G_1(bRec.wi, w_h) * G_1(bRec.wo, w_h);
const float denominator = 4.0f * Frame::cosTheta(bRec.wi) * Frame::cosTheta(bRec.wo) * Frame::cosTheta(w_h);
return (m_kd * INV_PI) + (m_ks * (D * F * G)) / denominator;
}파라미터인 bRec 안에 입사각 wi와 반사각 wo가 있고, 이 때 빛이 wi에서 wo방향으로 반사될 확률을 구하는 함수이다.
/// Evaluate the BRDF model
Color3f eval(const BSDFQueryRecord &bRec) const {
/* This is a smooth BRDF -- return zero if the measure
is wrong, or when queried for illumination on the backside */
if (bRec.measure != ESolidAngle
|| Frame::cosTheta(bRec.wi) <= 0
|| Frame::cosTheta(bRec.wo) <= 0)
return Color3f(0.0f);
/* The BRDF is simply the albedo / pi */
return m_albedo * INV_PI;
}이건 Diffuse 재질의 BRDF이다. wi와 wo에 관계없이 모든 방향에 대해 상수로 같은 확률을 갖는다.
'Dev > Theory' 카테고리의 다른 글
| 렌더링 방정식 (Rendering Equation) (0) | 2019.07.03 |
|---|---|
| 몬테카를로 적분 (Monte Carlo Integration, MC Integration) (0) | 2019.06.27 |
| 빛이 다른 매질로 갈 때 : 스넬의 법칙, 프레넬 계수 (Snell's Law, Fresnel Coefficient) (0) | 2019.03.12 |
| 밝기를 측정하는 방법 : Radiant Flux, Irradiance, Radiant exitance, Radiance (0) | 2019.02.22 |



